逐次２次計画法（SQP）

はじめに

状況に合わせて、どのように制御目標を指示し、システムを最適に稼働させるのかを決定するのもシステム制御の重要なテーマです。

逐次2次計画法(SQP)は非線形計画問題を解くソルバーです。逐次的に2次の部分最適化問題を解くアプローチです。このため、SQP（逐次２次計画法）ソルバーは、2次計画問題を解くQPソルバーを内包しています。

QPソルバーは、モデル予測制御(MPC)のソルバーとしても利用されています。
（QPソルバーについては、こちら →モデル予測制御(MPC) で紹介しています。）

逐次2次計画法のプログラムSQPは、組み込みも含めた幅広い利用用途があると思うので紹介していきます。

経緯

以前、システム制御の最適化を考えていた時に、非線形計画問題を解く必要があったので、逐次2次計画法(SQP)のアルゴリズムを岩波書店出版の「FORTRAN 77 最適化プログラミング」で学びました。

「FORTRAN 77 最適化プログラミング」には、代表的な数理計画法の計算アルゴリズムがFORTRANで掲載されています。

逐次2次計画法のプログラムもFORTRANで記述され掲載されていますが、以前、組み込み制御用にC言語に置き換えたプログラムを作成しました。非線形システムのソルバーとして、逐次2次計画法のプログラムSQPを活用していただける方もいるのではないかと思います。

ただし、著作物を利用して別の物を作成し、ブログで公開するなどの場合は著作権の侵害になります。原則として著作権者に無断で行うことは禁じられており、著作権者の許諾なく翻訳・翻案をすることはできません。

SQPプログラムのダウンロード

SQPのソースコード sqp.cppは、福島雅夫先生によるFORTRANのソースコードの美しさに比べると、乱雑稚拙なCソースコードで恥ずかしい限りですが、次のリンクからダウンロードできます。

　→ リンク

WindowsパソコンのVisual Studioで動作させています。

「FORTRAN 77 最適化プログラミング」に掲載のFORTRANで記述されたプログラムSQPのうち、入出力処理や表示のレベル処理、スケーリング処理およびコメント類はCソースには反映できていません。また、FORTRANからCに変更するにあたって、アルゴリズムも変更しているところがあります。

ご自由に活用頂いて構いませんが、利用により生じたトラブルの責任は負いかねます。

「FORTRAN 77 最適化プログラミング」（岩波書店）にはプログラムSQPのアルゴリズムが詳細に説明されています。詳細を知りたい場合は入手をご検討ください。また、大きな図書館には蔵書されていたりします。

SQPプログラム（ソースファイル）の使用方法

ソースファイル(sqp.cpp)には、テスト問題として(1)～(5)の５つの非線形問題を設定していますが、必要に応じてソースファイルを変更してください。

ソースファイル(sqp.cpp)のテスト問題(5)の目的関数と制約条件式を例に設定方法を説明していきます。

【 テスト問題(5) 】

　　目的関数：  \(f(x)  = x_1^2 - 4x_1 + x_2^2 - 2x_2 + 5\)

　　制約条件： \(c_1(x) = -x_1^2 + x_2 ≧ 0\)
 　　                 \(c_2(x) = -x_1 - x_2 + 2 ≧0\)

マクロ定義の設定

目的関数に含まれる変数の数をマクロ定義の N に設定します。
テスト問題(5)では、目的変数は \(x_1, x_2\) なので N=2 です。

等式制約条件式の数をマクロ定義の ME に設定します。
テスト問題(5)では、等式制約条件式はないので  ME=0 です。

不等式制約条件式の数をマクロ定義の MI に設定します。
テスト問題(5)では、不等式制約条件式は \(c_1(x), c_2(x)\) の 2式なので MI=2 です。

#define   N 2 // 変数の数 ( N>=ME )
#define   ME 0 // 等式制約条件式の数
#define   MI 2 // 不等式制約条件式の数

変数の数の最大値 NMAX、等式制約条件式の数の最大値 MEMAX、不等式制約条件式の数の最大値 MIMAX、制約条件式の数の最大値 MMAX、は共に10にしています。

目的関数、等式制約条件式、不等式制約条件式の設定

目的関数、等式制約条件式、不等式制約条件式をソースファイルの関数 fval() に設定します。
目的変数 \(x_n\) は、Cでは配列の添え字が 0 から始まるので配列 x[n-1] になります。また、配列をポインタ渡ししている関係で、x[n] ではなく vct(x,n) といった書き方にしています。

それぞれ、ソースコード上のコメントの(5)の後のコードになります。

目的関数の設定

目的関数： \(f(x)  = x_1^2 - 4x_1 + x_2^2 - 2x_2 + 5\)

 *objfun = vct(x,0)*vct(x,0)-4.0*vct(x,0)+vct(x,1)*vct(x,1)-2.0*vct(x,1)+5.0;

制約条件式の設定

等式制約条件式はありません。

不等式制約式： \(c_1(x) = -x_1^2 + x_2 ≧ 0\)
                        \(c_2(x) = -x_1 - x_2 + 2 ≧0\)

  vct(confun, 0) = -vct(x, 0) * vct(x, 0) + vct(x, 1);
  vct(confun, 1) = -vct(x, 0) - vct(x, 1) + 2.0;

各偏導関数の設定

次に偏導関数の設定が必要です。ソースファイルの関数 gval() に設定します。

目的関数の偏導関数の設定

　　目的関数： \(f(x)  = x_1^2 - 4x_1 + x_2^2 - 2x_2 + 5\)

より、偏導関数
\[\frac{\partial f(x)}{\partial x_1}=2x_1-4 \hspace{1cm} \frac{\partial f(x)}{\partial x_2}=2x_2-2\]を OBJGRA[] に下記ように設定します。

   vct(objgra, 0) = 2.0 * vct(x, 0) - 4.0;
   vct(objgra, 1) = 2.0 * vct(x, 1) - 2.0;

制約条件式の偏導関数の設定

制約条件式
        \(c_1(x) = -x_1^2 + x_2 ≧ 0\)
        \(c_2(x) = -x_1 - x_2 + 2 ≧0\)

の偏導関数
\[\frac{\partial c_1(x)}{\partial x_1}=-2x_1 \hspace{1cm}  \frac{\partial c_1(x)}{\partial x_2}=1 \\  \frac{\partial c_2(x)}{\partial x_1}=-1 \hspace{1cm}  \frac{\partial c_2(x)}{\partial x_2}=-1\]は CONGRA[][] に設定しますが、行方向に設定することに注意してください。
２次元配列の書き方は、mtx( congra, j, i ) になります。

mtx(congra, 0, 0) = -2.0 * vct(x, 0);  <-- \(c_1(x)\)の偏導関数
mtx(congra, 1, 0) = 1.0;                    <-- \(c_1(x)\)の偏導関数
mtx(congra, 0, 1) = -1.0;                   <-- \(c_2(x)\)の偏導関数
mtx(congra, 1, 1) = -1.0;                   <-- \(c_2(x)\)の偏導関数

初期値の設定

目的変数の数 N に応じて、x[]の初期値の設定が必要です。
関数 sqp() の最初に x[] の初期値の設定の処理があります。

初期値 0 としていますが、動作確認結果で示すように、初期値によっては計算条件を満たさず実行不可能となる場合もあるため、初期値の変更が必要となる場合があります。
また、初期値は最適解に近い方が演算回数が少なくて済むので、最適解がある程度想定できる場合は、近くに設定した方が良いです。

より大きなモデルを扱う場合

QPSOLVが実行可能解を持たない場合には、「②２次近似モデル 式(7.22) が実行可能解を持たない場合、ペナルティ関数の２次近似モデルを解く」が実行されます。その過程で、関数  auxqp() により係数行列を拡大する処理が行われます。大きなモデルを扱うと必要なメモリサイズも大きくなり、メモリが足りなくなる場合もあります。その時は、実行可能解を持たない場合、auxqp()以降の処理は行わず演算終了するように修正すれば、必要なメモリサイズを縮小することができます。 

動作確認結果

sqp.cpp のソースコードに入れている５つのテスト問題(1)～(5)の動作確認結果を示します。

Test Problem (1)

目的関数
        \(f(x)  = x^2 + 4x + 3\)
制約条件式
        \(c_1(x) = x - 1 ≧ 0\)
        \(c_2(x) = -x + 3 ≧ 0\)

結果

　\(x = 1.0 \)   目的関数値 8.0   OK 

Test Problem (2)

目的関数
        \(f(x)  = 3x_1^2 - 18 x_1 + 2x_2^2 - 8x_2\)
制約条件式
        \(c_1(x) = -3x_1 - x_2 + 9 ≧ 0\)
        \(c_2(x) = -3x_1 - 5x_2 + 15 ≧ 0\)
        \(c_3(x) = x_1 ≧ 0\)
        \(c_4(x) = x_2 ≧ 0\)

結果

　\(x_1 = 2.5, x_2 = 1.5 \)   目的関数値 -33.75   OK 

Test Problem (3)

目的関数
        \(f(x)  = 10x_1^2 - x_1 +10x_2^2\)
制約条件式
        \(c_1(x) = x_1^2+x_2^2 - 1 = 0\)
        \(c_2(x) = x_1 - 0.5 ≧ 0\)
        \(c_3(x) = x_2 + 0.5 ≧ 0\)

結果

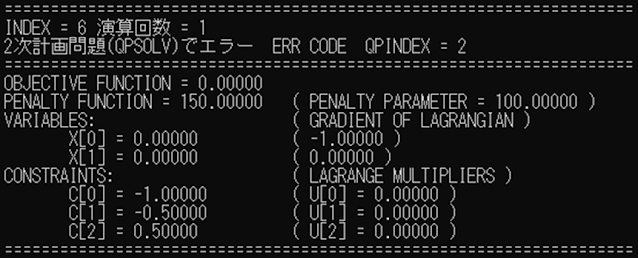
　初期値 \(x_1 = 0.0, x_2 = 0.0 \) では  エラー 
　QPSOLVで行列Gが正定値対称行列でないためQR分解不可(QPINDEX = 2)

　初期値を \(x_1 = 0.5, x_2 = 0.5 \) に変更
　\(x_1 = 1.0, x_2 = 0.0 \)   目的関数値 9.0   OK 

Test Problem (4)

目的関数
        \(f(x)  = x_1^2 - 28x_1 + x_2^2 - 20x_2 - 704\)
制約条件式
        \(c_1(x) = -x_1 - 2x_2 + 20 ≧ 0\)
        \(c_2(x) = -x_1 - x_2 + 15 ≧ 0\)
        \(c_3(x) = x_1 ≧ 0\)
        \(c_4(x) = x_2 ≧ 0\)

結果

　\(x_1 = 10.0, x_2 = 5.0 \)   目的関数値 -959.0   OK 

Test Problem (5)

目的関数
        \(f(x)  = x_1^2 - 4x_1 + x_2^2 - 2x_2+5\)
制約条件式
        \(c_1(x) = -x_1^2 +  x_2 ≧ 0\)
        \(c_2(x) = -x_1 - x_2 + 2 ≧ 0\)

結果

　\(x_1 = 1.0, x_2 = 1.0 \)   目的関数値 1.0   OK 

蛇足ですが・・・

最後までお読みいただき、ありがとうございました。

90年代の後半になると、クルマのパワープラントにハイブリッド技術が導入され、エンジン＋モーター＋エネルギーストレージ の組み合わせになりました。

エネルギーストレージが追加されることで、それまでなかった「時間方向の制御」の自由度ができました。

エネルギーストレージをどう使えばシステムを最適に稼働できるのか。

パワープラントの最適運転を考えるために数理計画の本を読み始めました。

このようなエネルギーストレージを使ったシステムの最適制御の考え方は、電力インフラにおける揚水式水力発電の活用にも見ることができます。

揚水式水力発電所では、夜間電力や一時的な余剰電力を使い水を汲み上げます。そして、ピーク時や需要変動時に水力発電を稼働させていますが、それってどういうこと？

次は電力インフラの最適運転を例に、非線形システムの最適化を考えます→次へ