はじめに
このブログでは、カルマンフィルタをどのように実装するのかを学びたい方を対象に、Excelでの演算処理の実施例とともにカルマンフィルタを説明していきます。
Excelファイルは、こちら からダウンロードできます。
ノイズや誤差を含む不確実な情報を扱うシステムでは、カルマンフィルタが広く利用されています。カルマンフィルタは、不確実な測定値の統計情報に基づいてシステムの状態を推定します。
具体的な適用例として、GNSSの測位情報にカルマンフィルタを適用し、測位精度を向上させている実施例が多くあるのはご存知かもしれません。
実際、GNSSの測位情報は、地上での移動体の制御に活用するには、そのままでは精度が不足していることが多いと思います。GNSSの電波を取得できる衛星の配置や衛星数、電離層やマルチパスの影響など測位情報の誤差要因は多くあります。
近年は、補正信号をSBASから取得して測位精度は改善されてきてはいるものの、利用の用途によっては、未だ十分とは言えないレベルであると思います。
適用を検討するシステム
GNSSの測位情報の精度向上が分かり易いと思うので、移動体の位置情報の精度向上について考えてみたいと思います。
実際の移動体の位置精度向上では、緯度経度の位置情報と、緯度方向と経度方向の移動速度と加速度の６つのパラメータでモデル化します。
このブログでは、もっと単純化して、ある地点を起点として、そこから一方向に一定速度で移動する移動体を考えます。一定速度なので加速度はなく、緯度経度の代わりに、起点からの一方向の移動（距離）だけを考えます。
移動地点の測位性能はGNSSと同等性能として、移動地点（距離）と速度について、カルマンフィルタで精度向上に取り組みます。
測位システムについて
- 測位システムは、平均0、標準偏差σ=10mの誤差を含む測位結果を返すものとします。
- 測位システムから移動速度も取得します。GNSSでは、移動体の速度を搬送波のドップラー効果で計測するため、測位よりも高精度に計測が可能です。平均0、標準偏差σ=0.3[m/s] の誤差とします。
システムのモデル化
カルマンフィルタでは、状態方程式と観測方程式でシステムをモデル化します。
観測方程式 \(y_k=Hx_k+{v}_k\)
カルマン先生が最初に提案したのが、上記の離散時間のモデルです。
状態方程式 \(x_{k+1}=Px_k+Qu_k\) の部分は、これまで扱ってきた離散化したシステムの逐次式と同じです。
\(w_k\) はシステム雑音、\(v_k\) は観測雑音を表しています。カルマンフィルタではノイズや誤差を確率変数として扱い、モデルの中に取り込んでいます。
今回このブログで扱う対象システムは、一方向に一定速度で移動する移動体。移動速度を\(V\)、移動距離を\(S\)、加速度は \(0\) とすると\[\hspace{0.2cm}\text{加速度}\hspace{0.5cm} \frac{dV}{d t}=0 \hspace{0.5cm} \text{速度}\hspace{0.5cm}\frac{dS}{d t}=V\]状態方程式は下記になります。
\[ \frac{d}{dt} \left[ \begin{array}{l}
S \\
V
\end{array} \right]= \left[ \begin{array}{cc}
0 & 1 \\
0 & 0
\end{array} \right]
\left[ \begin{array}{c}
S \\
V \end{array} \right]
+\left[ \begin{array}{c}
0 \\
0 \end{array} \right] u \hspace{0.5cm} \text{（一定速度のため入力なし）}\]
この状態方程式を、Excelのシート【状態方程式】で離散化した逐次式に変換しています。
離散化時間は ΔT=1秒 です。
これまで扱ってきた手法（参考→離散化）と同じです。
状態変数 \(x_k\) は移動距離 \(S_k\) と移動速度 \(V_k\) のベクトルです。
\[x_k=\left[\begin{array}{l}S_k \\ V_k\end{array}\right] \]
Excelのシート【カルマンフィルタ】では、初期位置は \(S_0\) = 0、移動速度\(V_k\)=10[m/s]（一定）としています。
行列\(G,H\)は単位行列です。
行列\(P\)は Excelのシート【状態方程式】で求めた逐次式の値を参照しています。
また、\(u_k\) はシステムへの入力ですが、今回の移動体のモデルでは入力がないので、状態方程式の演算式では入力の項 \(Qu_k\) を省略しています。
\(w_k\)はシステム雑音、\(v_k\)は観測雑音です。
\[w_k=\left[\begin{array}{l}w_{sk} \\ w_{vk}\end{array}\right] \hspace{1cm} v_k=\left[\begin{array}{l}v_{sk} \\ v_{vk}\end{array}\right] \]
システム雑音\(w_k\)、観測雑音\(v_k\)の確率的な特性は既知であることが前提です。
測位システムの条件から、観測雑音 \(v_{sk}\) は、平均0、標準偏差σ=10[m]、同様に\(v_{vk}\) は、平均0、標準偏差σ= 0.3[m/s]とし、正規乱数（正規分布した乱数）をそれぞれExcelの関数で自動生成しています。
システム雑音 \(w_{sk}\) と \(w_{vk} \)は、観測雑音\(v_{sk}\) と \(v_{vk} \)よりも相対的に小さくなるように、平均0、標準偏差σ=0.1 にしています。
カルマンフィルタによる状態推定
カルマンフィルタは、モデルによる予測値の算出（事前推定）と観測値による予測値の修正（事後推定）を繰り返し、システムの状態推定を進めていきます。
予測値算出（事前推定）
予測値算出（事前推定）の過程では、状態方程式でシステムの状態を推定します。推定するのはシステムの状態変数 \(\hat{x}_{k|k-1}\) とシステムの推定誤差 \(\hat{\Sigma}_{k|k-1}\) です。
演算式は下記の①②です。
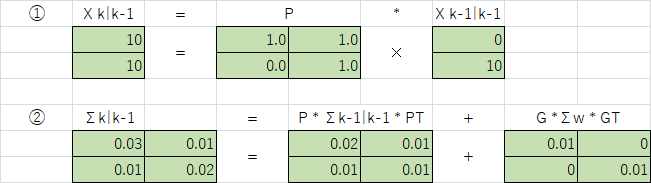
① \(\hat{x}_{k|k-1}=P\hat{x}_{k-1|k-1}+Qu_{k-1}\)
② \(\hat{\Sigma}_{k|k-1}=P\hat{\Sigma}_{k-1|k-1}P^T+G{\Sigma}_{w}G^T\)
ここで、^は推定値、\(\hat{x}_{k|k-1}\) は、時刻 k-1 までの観測値に基づく時刻 k の状態変数 \(x\) の推定値を表しています。今回の移動体のモデルでは入力がないので、\(Qu_{k-1}\)の演算は省略しています。
システムの誤差について
システムの状態変数 \(x_k\) に複数の確率変数が含まれる場合、システムの誤差は共分散行列になります。状態変数 \(x_k\) が、移動距離 \(S_k\) と移動速度 \(V_k\) のベクトルの場合、
\[x_k=\left[\begin{array}{l}S_k \\ V_k\end{array}\right] \]
移動距離 \(S_k\) と移動速度 \(V_k\) の標準偏差を \(σ_s\)、\(σ_v\) とすると、その共分散行列は、
\[{\Sigma}=\left[\begin{array}{ll}{σ_s}^2 & σ_s σ_v \\ σ_s σ_v & {σ_v}^2\end{array}\right]\]
になります。移動距離 \(S_k\) と移動速度 \(V_k\) が独立した（互いに依存関係のない）確率変数の場合は、対角行列以外の \(σ_s\) \(σ_v\) の項は０に収束するため、対角行列にシステムが含む確率変数の分散値が並ぶ行列になります。
\[{\Sigma}=\left[\begin{array}{ll}{σ_s}^2 & 0 \\ 0 & {σ_v}^2\end{array}\right]\]
観測値による予測値の修正（事後推定）
観測値による予測値の修正（事後推定）の過程では、予測値算出（事前推定）の過程で推定したシステムの状態変数 \(\hat{x}_{k|k-1}\) とシステムの推定誤差 \(\hat{\Sigma}_{k|k-1}\) を観測値 \(y_k\) を用いて補正します。
演算式は下記の③④⑤です。
③ カルマンゲイン
\[Kg=\frac{\hat{\Sigma}_{k|k-1}H^T}{H\hat{\Sigma}_{k|k-1}H^T+{\Sigma}_{v}}\]
④ \(\hat{\Sigma}_{k|k}=\hat{\Sigma}_{k|k-1}-KgH\hat{\Sigma}_{k|k-1}\)
⑤ \(\hat{x}_{k|k}=\hat{x}_{k|k-1}+Kg(y_k-H\hat{x}_{k|k-1})\)
⑤の式は、入力がないシステムのオブザーバの演算式と同じです。（オブザーバ→こちら）オブザーバもシステムの内部状態を推定する機構です。オブザーバでは、オブザーバゲインをシステムの安定条件から定めました。
一方、 ⑤の式のKgはカルマンゲインとよばれ算出式は③です。
カルマンゲインは、推定値と観測値 \(y_k\) との偏差を、どの程度 \(\hat{x}_{k|k-1}\) と \(\hat{\Sigma}_{k|k-1}\) に反映させるかを決めています。③の式を見ると、カルマンフィルタでは、その割合を情報の確からしさ（ \(\hat{\Sigma}_{k|k-1}\) と \({\Sigma}_v\) ）で決定します。
今回のシステムでは、システム雑音 \(w_{sk}\) の標準偏差 \(σ_{ws}\)（0.1[m]）に対し、観測値 \(y_k\) に含まれる観測雑音 \(v_{sk}\) の標準偏差 \(σ_{vs}\)（10[m]）を相対的に大きくしています。これは、観測値 \(y_k\) の確からしさを低く設定することにより、観測値のバラつきの反映を制限することを意図しています。
Excelファイル
上記のカルマンフィルタ適用のExcelファイルは、こちら からダウンロードできます。
Excelファイルのシート「カルマンフィルタ」では、状態方程式と観測方程式、①～⑤のカルマンフィルタによる状態推定を計算しています。グレーのハッチングのセルは中間演算値です。セルC2には計算回数を設定します。計算回数設定セルの右側の「計算開始」ボタンで計算を開始します。
VBAで、状態変数 \(x\)の更新と、計算した \(\hat{x}_{k|k}\) と \(\hat{\Sigma}_{k|k}\) を \(\hat{x}_{k-1|k-1}\) と \(\hat{\Sigma}_{k-1|k-1}\) のセルに上書きすることで繰り返し演算を回しています。
システム雑音 \(w_{sk}\) 、観測雑音 \(v_{sk}\)は、Excelの関数で正規乱数を自動生成しています。
計算結果は、位置と速度の観測値と推定値をシート「結果」に書き出しています。
結果
カルマンフィルタの処理結果を示します。
今回のシステムの課題は、観測値 \(y_k\) に含まれる観測雑音 \(v_{sk}\) が非常に大きく、測位結果をそのまま使えないことでした。
そのため、カルマンフィルタの \(Σ_v\) と \(Σ_w\) の設定において、観測雑音の影響を受けないように、\(σ_{ws}\) ≪ \(σ_{vs}\) としてカルマンゲインが小さくなるようにしています。
設定意図の通り、結果のグラフでは、測位位置の推定値は観測した測位値の影響を受けずに、ただし、測位値の傾向は追従する推定結果になります。
Excelファイルでは初期値は下記のようにしています。
カルマンフィルタでは、意図する動作に合わせたパラメータ設定がポイントになります。
最後まで読んでいただきありがとうございました。
カルマンフィルタの理解のお役に立てましたでしょうか。
0 件のコメント:
コメントを投稿