はじめに
ここまで、システムの内部の振る舞いを状態方程式で記述し、その時間応答を確認してきました。しかし、システムによっては内部を物理式で記述することが難しい場合もあります。そのような場合は、システムの入力に対する出力の挙動データからシステムの振る舞いを定式化することもできます。
システム同定とは入出力データからシステムの振る舞いを表現した数式モデルを導き出すことです。ここでは、以下の内容を確認してシステム同定が使える知識になるように説明しようと思います。
- インパルス応答の基本的な概念とシステム同定モデルの例
- システム応答の計算方法である畳み込み演算(convolution)
- 車両走行モデルとバネマスモデルでのシステム同定の確認
システム同定したモデルは、シミュレーションに使えるだけでなく、制御にも応用可能です。このブログでは、この後の「制御」でシステム同定したモデルをフィードフォワード制御に利用する例を示します。
インパルス応答の基本的な概念
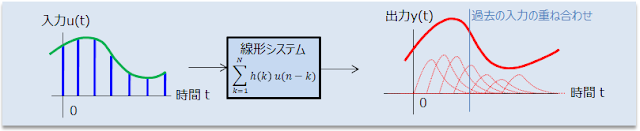
インパルス応答の復習です。インパルス信号は時間0の微小な領域だけで0以外の値を持ち、積分すると 1 になる信号です。インパルス信号を入力したときのシステムの応答がシステムのインパルス応答になります。
入力信号u(t)をインパルス信号の組み合わせと考えると、線形システムではその応答もインパルス応答の重ね合わせになります。
出力応答は、入力信号とインパルス応答の畳み込み演算(convolution)で計算できます。
\[y(n)=\sum_{k=1}^{N} h(k) u(n-k) \]
システム同定のモデル
インパルス応答は入力信号の重ね合わせで表現する数式モデルですが、出力信号も利用するモデルもあります。
MAモデル
インパルス応答のように、システムへの過去の入力の重ね合わせで表現したモデルは、MAモデルとよびます。過去N個の入力が使われている場合はN次のモデルとよびます。
\[y(n)=\sum_{k=1}^{N} h(k) u(n-k) \]
ARモデル
システムの挙動を過去の出力の重ね合わせで表現したモデルは、ARモデルとよびます。
ARMAモデル
システムの挙動を過去の入力と出力の重ね合わせで表現したモデルは、ARMAモデルとよびます。
\[y(n)=\sum_{k=1}^{p} a(k) y(n-k)+\sum_{k=1}^{q} b(k) u(n-k)\]
このブログでは、逐次式との比較が容易なARMAモデルによるシステム同定を考えていきます。ARMAモデルのシステム同定とは、具体的にはシステムの入力に対する出力の挙動データから、数式モデルの 𝑎(𝑘), 𝑏(𝑘) を決定することになります。
EXCELファイルのダウンロード
こちらからシステム同定のEXCELファイルをダウンロードできます。
システム同定のEXCELファイルには、システムの入力と出力の応答データから、ARMAモデルのパラメータ 𝑎, 𝑏 を最小二乗法で逐次的に推定する処理を組み込んでいます。
車両走行モデルやバネマスモデルの入力と出力の応答データから、システム同定する例を各シートに示しています。
入力と出力の応答データ U(N), Y(N) に別のシステムの応答データを設定すれば、そのシステムのARMAモデルのパラメータ 𝑎, 𝑏 を求めることができます。
システム同定Excelシートの説明
- 次数の設定でARMAパラメータ a, b の数を2~20の範囲で指定します。4を指定すると a1,a2,b1,b2 の2次のモデルとして計算します。
- 入出力データは赤枠内の 入力U(N), 出力Y(N) に設定します。最大1000データまで設定可能です。設定したデータ数に合わせて入出力データ数も更新してください。
- 設定した入力データ数分の逐次演算を実行しますが、収束が不十分な場合は繰り返し演算回数の設定(C4 のセル)で演算回数を増やして、システム同定の収束を高めることができます。
- ARMAパラメータ推定のボタンで計算処理を開始します。計算結果は青枠内のセルに表示されます。
- システム同定の収束レベルは、緑枠の誤差の積算値とグラフで確認します。グラフ上で設定した出力Y(N)とARMAモデルの出力Y(N)が重なればOKです。
こんな感じで動きます
畳み込み演算(コンボリューション)
システム応答の畳み込み演算(convolution)をEXCELシート上で確認します。
3次のモデルの場合、過去3回の入出力データと a, b のパラメータの畳み込み演算で次の出力を計算します。EXCELシート上では下の図のような計算になります。
システム同定の確認
車両走行モデル ~加減速の挙動
システム同定(走行 加速度)のシートでは、状態方程式でモデル化した車両の加減速の挙動データを用いて車両の加減速のARMAモデルを同定します。
車両走行モデルの加速度は1次遅れのモデルにしたので、次数は1(パラメータ数2)でARMAのパラメータ同定を実行しています。1次遅れのモデルについてはこちらを参照して下さい。1次遅れモデルで\[e^{-\frac{\Delta t}{T}}=\alpha \] とすると逐次式は \[𝑥(𝑘+1) = \alpha x(k)+(1−\alpha)u(k)\] 時定数1sec, 離散時間100ms より
\[\mathrm{A} 1=\alpha=e^{-\frac{\Delta t}{T}}=0.9048 \ldots \]\[\mathrm{B} 1=1-\alpha=0.0951 \ldots \]であり、1次遅れの真値と比べると若干の誤差はあるものの、グラフからも分かるように、ほぼ同定できています。
車両走行モデル ~速度の挙動
システム同定(走行 速度)のシートでは、状態方程式でモデル化した車両の加減速の挙動データを用いて、車両の速度のARMAモデルを同定します。特性が分かっていないシステムを同定する場合は、次数を増やしたり、演算回数を増やしてみて、同定パラメータの誤差の収束状況を確認します。不必要にパラメータの次数は上げず、なるべく少ない次数でのシステム同定を目指します。
バネマスモデル ~変位速度の挙動
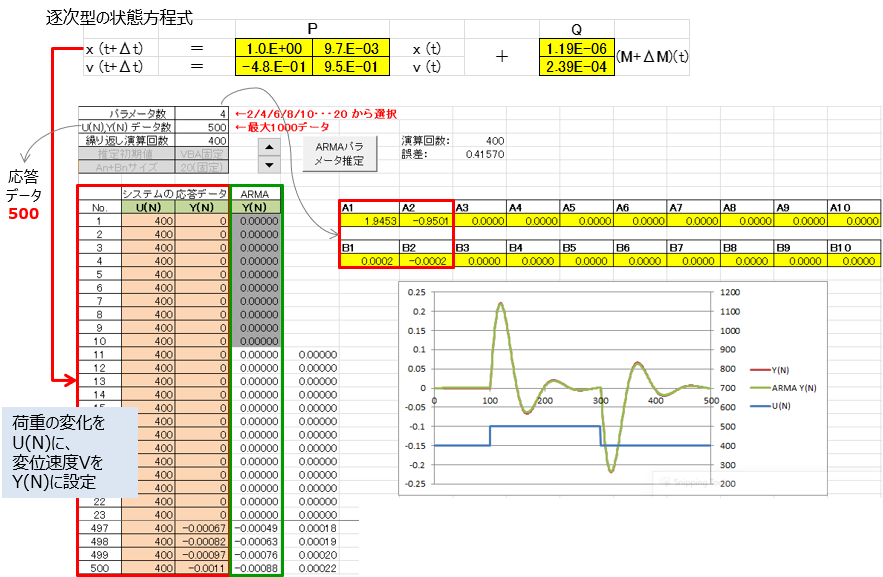
システム同定(バネマス 変位速度)のシートでは、状態方程式でモデル化したバネマスモデルの荷重変化時の変位速度の挙動データを用いてARMAモデルを同定します。
システム同定(バネマス ストローク)のシートでは、状態方程式でモデル化したバネマスモデルの荷重変化時の変位量(ストローク量)の挙動データを用いてARMAモデルを同定します。
挙動データの変化が少ない場合、逐次推定で必要となる演算回数が増えます。繰り返し演算回数を増やすと演算時間も長くなるので注意が必要です。
ARMAモデルパラメータの逐次推定方法
ARMAモデル
\[y(n)=\sum_{k=1}^{p} a(k) y(n-k)+\sum_{k=1}^{q} b(k) u(n-k)\]において
\[x=\left[a_{1}, a_{2}, \cdots \cdot, a_{p}, b_{1}, b_{2}, \cdots \cdot, b_{q}\right]^{T} \] \[z(n)=[y(n-1), \cdots, y(n-p), u(n-1), \cdots, u(n-q)]^{T} \]\[Z=\begin{bmatrix} z^{T}(n+1) \\ \vdots \\ z^{T}(N) \\ \end{bmatrix} \]\[P_N=({Z_N}^{T} Z_N)^{-1} \]としたときに、最小二乗法で逐次的に 𝑥 を推定するアルゴリズムは\[\hat{x}_{n+1}=\hat{x}_{n}+g(n+1)\left\{\mathrm{y}(n+1)-z^{T}(n+1) \hat{x}_{n}\right\}\]\[g(n+1)=\frac{P_{n} z(n+1)}{1+z^{T}(n+1) P_{n} z(n+1)}\]\[P_{n}=\left[I-g(n) z^{T}(n)\right] P_{n-1}\]です。
EXCELには、このアルゴリズムをVBAのmodule1に実装しています。EXCELの「開発」タグを選択し、「Visual Basic」からプログラムを確認できます。
VBAのコードは、適応制御(セルフチューニングレギュレータ)で提示しています。
最後までお読みいただき、ありがとうございました。


















0 件のコメント:
コメントを投稿