非線形なシステムへの対応　～地球の運動について

はじめに

チ。地球の運動について　再放送も見てます。

こんなに合理的に、動いてしまったら、この説を、美しいと、 思ってしまう !!
　　by ラファウ　

・・・ということで、地球と月の軌道を状態方程式にして、非線形系のシミュレーションの例として書いてみようと思います。

目的（そもそも、なぜ状態方程式にする？）

天体の軌道をシミュレーションする場合、ルンゲクッタ法を使う事が多いと思います。シミュレーションの精度でもルンゲクッタ法が良いはずです。ただ、このブログでは、制御工学の組み込み方法にフォーカスしているので、敢えて天体の軌道を状態方程式にして、シミュレーションで確認していきます。例えば、衛星の観測軌道をカルマンフィルタで補正する場合は、衛星の軌道モデルを状態方程式にする必要があるように、非線形系のモデルを状態方程式にする例として説明します。

ダウンロード

Excelファイルはこちら→リンク
⑧-2 非線形モデル 地球を動かす.xlsm です。

太陽と地球と月の間の引力

質量m1とm2の間の万有引力は下記の式になります。

\[F=G \frac{m_{1} m_{2}}{r^2} [N]\]

\(G\)は万有引力定数で、\( G=6.672\times 10^{-11} [m^{3}kg^{-1}s^{-2}] \) です。万有引力は質量と距離で決まります。

太陽と地球と月の間の引力を考えてみると、地球や月は若干楕円軌道で、月は地球の周りを公転しているので位置関係が変わります。また、太陽と地球の公転軌道に対して、月の公転軌道面が若干（5.1度）ズレており、　万有引力は相互に作用するため厳密に考えると非常に複雑で非線形な関係です。

太陽の質量を\(M_{s}\), 地球の質量を\(M_{e}\), 月の質量を\(M_{m}\),
太陽と地球の距離を\(L_{se}\), 地球と月の距離を\(L_{em}\) とすると、地球に作用する引力は、

\[F_{e}= -G \frac{M_{s} M_{e}}{{L_{se}}^2} + G \frac{M_{e} M_{m}}{{L_{em}}^2}\hspace{1cm}[N]\]

太陽と月の距離を\(L_{sm}\)とすると、月に作用する引力は、

\[F_{m}= -G \frac{M_{s} M_{m}}{{L_{sm}}^2} - G \frac{M_{e} M_{m}}{{L_{em}}^2}\hspace{1cm}[N]\]

さらに、地球の移動速度を\(V_{e}\), 月の移動速度を\(V_{m}\) とすると、

\[F_{e}=M_{e} \frac{dV_{e}}{dt}\hspace{1cm}F_{m}=M_{m} \frac{dV_{m}}{dt}\]

より

\[ \frac{dV_{e}}{dt}= -G \frac{M_{s}}{{L_{se}}^2} + G \frac{M_{m}}{{L_{em}}^2} \tag{1} \]
\[ \frac{dV_{m}}{dt}= -G \frac{M_{s}}{{L_{sm}}^2} - G \frac{M_{e}}{{L_{em}}^2} \tag{2} \]

太陽の質量は地球の33万倍もあり、地球や月から太陽への引力の影響は無視することにして複雑さを排除します。さらに、太陽と地球の公転軌道と月の公転軌道は同一平面とし、2次元平面 \((X,Y)\) で考えていきます。

地球の座標を \((X_{e},Y_{e})\)、月の座標を \((X_{m},Y_{m})\)  とすると、移動速度の\(X, Y\) 成分は、

\[\frac{dX_{e}}{dt}=V_{ex} \hspace{1cm} \frac{dY_{e}}{dt}=V_{ey}\]

\[\frac{dX_{m}}{dt}=V_{mx} \hspace{1cm} \frac{dY_{m}}{dt}=V_{my}\]

また、

    太陽と地球の距離    \(L_{se}=\sqrt{{X_{e}}^2+{Y_{e}}^2}\)

    太陽と月の距離        \(L_{sm}=\sqrt{{X_{m}}^2+{Y_{m}}^2}\)

    地球と月の距離        \(L_{em}=\sqrt{ {(X_{m}-X_{e})}^2 + {(Y_{m}-Y_{e})}^2 }\)

になるので、式(1) (2)を \(X, Y\) 成分に分けて記述すると

\[ \frac{dV_{ex}}{dt}= -G \frac{M_{s}}{{L_{se}}^2}\frac{X_{e}}{L_{se}} + G \frac{M_{m}}{{L_{em}}^2}\frac{(X_{m} -X_{e})}{L_{em}} \tag{3} \]

\[ \frac{dV_{ey}}{dt}= -G \frac{M_{s}}{{L_{se}}^2}\frac{Y_{e}}{L_{se}} + G \frac{M_{m}}{{L_{em}}^2}\frac{(Y_{m} -Y_{e})}{L_{em}} \tag{4} \]

\[ \frac{dV_{mx}}{dt}= -G \frac{M_{s}}{{L_{sm}}^2}\frac{X_{m}}{L_{sm}} - G \frac{M_{e}}{{L_{em}}^2}\frac{(X_{m} -X_{e})}{L_{em}} \tag{5} \]

\[ \frac{dV_{my}}{dt}= -G \frac{M_{s}}{{L_{sm}}^2}\frac{Y_{m}}{L_{sm}} - G \frac{M_{e}}{{L_{em}}^2}\frac{(Y_{m} -Y_{e})}{L_{em}} \tag{6} \]

状態方程式に

微分方程式を状態方程式にまとめます。

\[ \frac{d}{dt}  \begin{bmatrix}  X_{e}\\Y_{e}\\X_{m}\\Y_{m}\\V_{ex}\\V_{ey}\\V_{mx}\\V_{my} \end{bmatrix} = \begin{bmatrix}
 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\
 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
 Equ1  & 0 & Equ2 & 0 & 0 & 0 & 0 & 0 \\
 0 & Equ1 & 0 & Equ2 & 0 & 0 & 0 & 0 \\
 Equ3 & 0 & Equ4 & 0 & 0 & 0 & 0 & 0 \\
 0 & Equ3 & 0 & Equ4 & 0 & 0 & 0 & 0 \end{bmatrix}
\begin{bmatrix}  X_{e}\\Y_{e}\\X_{m}\\Y_{m}\\V_{ex}\\V_{ey}\\V_{mx}\\V_{my} \end{bmatrix}  + \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} U\]

\[ Equ1= -G \frac{M_{s}}{{L_{se}}^3} - G \frac{M_{m}}{{L_{em}}^3}\]

\[ Equ2= G \frac{M_{m}}{{L_{em}}^3}\]

\[ Equ3= G \frac{M_{e}}{{L_{em}}^3}\]

\[ Equ4= -G \frac{M_{s}}{{L_{sm}}^3} - G \frac{M_{e}}{{L_{em}}^3}\]

引力の関係だけなので入力 \(U\) はありません。
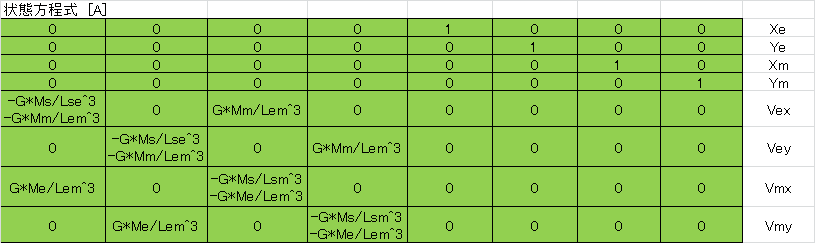
Excelファイルでは、シート【状態方程式】で状態方程式の行列 \(A\) を定義しています。

モデルの線形化について

状態方程式の行列 \(A\) には、距離 \(L_{se}, L_{sm},L_{em}\) が含まれています。
太陽と月の距離は、月の公転に従って変化するだけでなく、各距離は相互の引力の影響で微妙に変化するため非線形なモデルです。

一般的に非線形なモデルを線形化する場合、各動作点において非線形特性を一次式で線形近似します。最初のステップでは、そのように各動作点において線形近似して、離散化処理を行ってみましたが、私の旧型PCではあまりにも演算時間がかかってしまうので、そのアプローチは断念し、距離 \(L_{se}, L_{sm},L_{em}\) を一定としました。太陽と月の距離も平均的には太陽と地球の距離と同じとしています。

距離を一定とした段階で円軌道になることを前提としているではないか！

これを近似と言っていいのか？かなり疑問ですが、今回はそのような極めて簡易的な方法で状態方程式を線形化しています。

状態方程式にまとまれば、これまでやってきたように離散化していきます。

状態方程式を離散化

状態方程式

\[\frac{d x(t)}{d t}=A x(t)+B u(t) \]

を以下のように離散化します。

\[x(t+Δt)=Px(t)+Qu(t)\]\[P=I+AΔt(I-\frac{Δt}{2}A)^{-1}\]

\[Q=Δt(I-\frac{Δt}{2}A)^{-1}B\]

離散化の手法については、こちら→リンク で説明しています。
Excelファイルでは、シート【状態方程式】で以下のように計算しています。

単位系について

通常単位系はSI単位系を使いますが、扱う数値が大きいので、単位系を変更しています。

単位時間：10000秒、単位距離：10000km、質量：kg、速度：km/秒

各パラメータは以下の通り

月の速度の初期値は、地球の公転速度＋月の公転速度 です。

シミュレーション

Excelファイルのシート【シミュレーション】の【軌道計算】ボタンで計算を開始します。演算回数 3154回 は、離散化時間 10000秒 で1年になります。演算回数は データサイズ の 3154 のセルで変更できます。【STOP】ボタンをクリックすると計算は止められます。

月の軌道は、このサイズの図では地球の軌道と重なって見えないので、地球との距離を15倍にして表示しています。

シート【状態方程式】で計算した離散化した行列 \(P\) をシート【シミュレーション】で使っています。制御入力 \(U\) はありません。軌道を表示しているExcelのグラフは散布図です。VBAで順次、地球と月の (N+1) 軌道計算データを散布図の表示セルに格納します。その後、そのデータで(N)のセル（下図の赤のセル）を更新し、順次軌道データ (N+1) を計算していきます。

月の軌道については、地球の公転軌道の内側に入るケースと、外側に出るケースで表示順番を変えたデータ系列を作り、それぞれに格納することで、月の軌道を多少立体的に見せています。

初期条件として、位置と質量、移動速度を与えただけなのに、地球と月は１年かけて太陽を周回する軌道になりました。当たり前なんですが。。。

特に月の軌道については、こんな軌道だったんだ と再認識。月は地球を回っているもんだと思っていましたが、そんなに単純ではないようで、その軌道を知ると月の存在の尊さを感じます。